- VIBRATING BODIES & ACOUSTIC SPECTRA
ILONGITUDINAL VIBRATION
This is where the vibrational forces and displacements occur in the direction of the wave propigation, eg. in a column of air such as a woodwind instrument or along the string of a guitar or violin (where the tension forces act in the direction of the axis of the string). Perhaps the most important of all longitudinal vibrating systems is the human voice.
|
An example of longitudinal vibration is a long spiral string with a compression pulse travelling along it. More pulses need to be applied with the right timing to set up a standing wave because friction quickly damps the first pulse. |
|
A representation of the harmonic waveforms of a string. The tension waves in a string are easy to see. When a string is plucked reflections of the pulse reflect from both ends and create standing waves which are as long as the whole string or integer fractions of the string length (ie. 1/2, 1/3, 1/4 length etc.). |
The string doesn't move at the points where the waveform crosses the straight line. These are called node points. Since the frequency of vibration of such waves is inversely proportional to their wavelength, overtones or partial frequencies occur at integer multiples of the fundamental (lowest) frequency of the string (ie. 2, 3, 4 times etc). When overtones are integer multiples of the fundamental they are known as harmonics.
The acoustic spectrum of a vibrating object is the recorded amplitudes (pressures of radiated air waves) for the various partial frequencies over a certain time. These amplitudes may be effected by the type of excitation of the vibrations, the efficiency with which the vibrational energy of the object is transferred to the surrounding air, and the internal damping of vibration in the object itself.
The timbre of a sound is closely related to its acoustic spectrum. For example different speech vowels often contain the same overtones with different amplitudes.
|
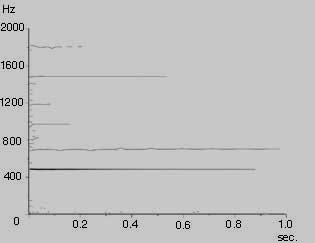
This graph shows the harmonics of my voice speaking the words "Australian Bell". Frequency (Hz) is the vertical axis and time is the horizontal axis. The amplitude of each harmonic is shown by the darkness of the line. Notice the differences between the vowels AU, A, I, and E in this sentence (for an Australian accent!). |
FLEXURAL VIBRATION
This is where the vibrational displacements are not in the direction of propigation, eg. when a xylophone bar is struck in its center the initial displacement is in the direction of the mallet head but the wave propigation is along the length of the bar.
The physics of flexural vibrations are such that the overtones do not naturally lie in harmonic relationships. For the more technically minded this is because they occur in dispersive media where the velocity of the wave varies with its frequency (so the reflected impulses don't occur twice as quickly, even if the wavelength is halved). Most flexural vibrations are too complex to describe by a single mathematical formula, so complex computer programs involving thousands of mathematic equations are now used to describe them.
The following images show three of the types of vibration found in bells, the 2,0, 3,0 and 2,1 modes. The first number refers to the the number of vertical nodal lines (lines along the surface of the object that don't move in this mode of vibration), and the second number refers to the number of horizontal nodal lines. The blue color is the part of the bell that vibrates with the least amplitude and the red vibrates with the greatest amplitude. We call modes with only vertical nodal lines (eg. 2,0 mode) circumferential modes, modes with only horizontal nodal lines axial modes, and modes with both horizontal and vertical nodal lines (eg. 2,1 mode), mixed modes.
 |
 |
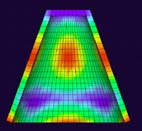 |
2,0 mode |
3,0 mode |
2,1 mode |
Sounds where the frequencies of the overtones are not in harmonic relationships are described as inharmonic.
 |
This graph shows partial frequencies in the sound of a gong. |
- MUSICAL PERCEPTION OF PITCH & HARMONY
PITCH
Perception of pitch can be likened to attempting to sing an imitation of the sound you hear.
HARMONIC SOUNDS
This is relatively easy when a sound is comprised of just one frequency or a series of harmonics (such as a guitar or clarinet sound). In these cases the harmonics of the voice can be varied until they form a one to one relationship with the sound. Often we don't actually vocalise this imitation, it simply remains as a response or perception in our mind.
In some cases we can't hear the complete sound because certain frequencies are not loud enough, or are masked by other sounds occuring simultaniously. When this occurs our perceptual systems simply assume the missing frequencies are there based on experience. This causes the perceptual phenomenon known as virtual pitch, where the pitch of a sound is attributed to the fundamental tone of the perceived harmonics, even though the fundamental was never actually sounded. This happens when you listen to a double bass recording through a small loudspeaker that can't produce low frequency sounds.
INHARMONIC SOUNDS
The pitch perception of inharmonic sounds arising from flexural vibrations is more complex.
 Try pitching your voice to the sound of a cymbal or the gong sound. Try pitching your voice to the sound of a cymbal or the gong sound.
 |
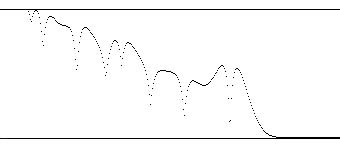
In the example of a cymbal you may find many pitches you can sing that to some extent match the sound. Since the cymbal sound doesn't have harmonics (unless by some rare accidental relationships) you will be picking out the loudest individual overtones to sing to.
The gong sound has fewer overtones than a cymbal, and if you look closely at the spectrum you will notice that there are some overtones at frequencies in almost harmonic relationships above a missing fundamental at about 240Hz. Therefore this sound has a strong pitch perception centered around 240Hz as well as a number of other weaker pitch perceptions.
|
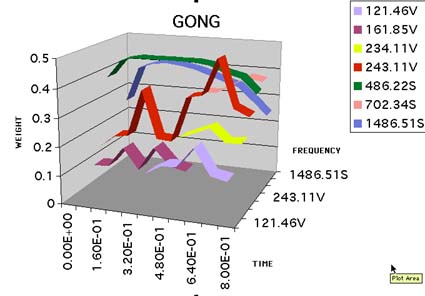
This graph shows a computer model of pitch perception resulting from a small gong (produced by Denzil Cabrera's Psy-sound software). The 243, 162 and 121 Hz virtual percepts are subharmonics of the 486 Hz spectral percept and the 234 virtual is a subharmonic of the 702 spectral percept. All the spectral percepts are close to harmonics of 243 Hz which becomes the strongest pitch percept after about 0.5 seconds. Other partial frequencies visible in the spectrum shown earlier are not audible because they are masked by the stronger partials shown here.
Of course bells also vibrate flexurally and so until the recent invention of the harmonic bell, also had inharmonic overtones and confusing pitch percepts.
HARMONY
The perception of harmony is also very dependent on the timbre of a sound.
If we confine ourselves to thinking about the relative consonance and dissonance between certain sounds we can reveal a relationship between a sound's timbre and the pitches of that sound that produce harmony when heard simultaniously. Dissonance is caused when frequencies in one sound are only slightly different from the frequencies of another.
Slight differences in frequency between two sounds produce beating as the two sounds move from being 'in phase' to 'out of phase' with each other. This is heard when tuning string instruments. In phase sounds have concurrent peaks and valleys and so add their amplitudes. Out of phase sounds have peaks concurrent with valleys and so cancel out each others amplitudes. If two sounds have slightly different frequencies they move in and out of phase and so cause beating at a frequency equal to the frequency difference between the two sounds. When the beating becomes to quick to be heard it produces a perception of roughness or dissonance between the two sounds.
|
|
 |
Comparison of 200Hz and 300Hz harmonic sounds
The minimum dissonance (or maximum consonance) between sounds with harmonic overtones occur when one sound is in a simple frequency ratio with the other.
In this example two harmonic sounds are at a frequency ratio of 3/2 (an interval of a fifth in the Western scale). Alternate harmonics of Sound 2 are either at the same frequency or half way between the harmonics of Sound 1, thus minimising dissonance between the two sounds. In certain circumstances these two sounds may appear to fuse producing a sound with many of the harmonics of a 100 Hz harmonic sound. The fundamental and prime number harmonics above 3 are missing from the harmonic series starting at 100 Hz and so this composite sound is an example of virtual pitch.
|
|
An example of a dissonance curve showing minima at consonant intervals (with thanks to Terry McDermott).
Just tuning is a musical tuning system that uses integer frequency ratios of harmonic sounds to maximise consonance. Harry Partch (see Genesis of a Music, Da Capo Press ) describes a tuning system that uses all the possible ratios of integers up to 13. Most musical systems that use instruments producing harmonic sounds have evolved through using integer ratio tunings.
Recently William Sethares devised a method of calculating tuning ratios that minimised the dissonances between inharmonic sounds (see Tuning, Timbre, Spectrum and Scale, Springer-Verlag, 1998). This was achieved by calculating and summing the roughness between each overtone of the sounds for incremental changes in the tunining ratios. In his book he provides a theory for the tuning systems used in Indonesian gamelan derived by minimising the dissonances between gongs and the human voice.
|
Harmony in Western music has been complicated by the desire to modulate chords and melodies; that is, to play the same set of ratios starting at different fundamental frequencies. The logical conclusion of modulation is to produce an equally spaced array of fundamental frequencies known as the equally tempered scale. This scale, while mathematically very simple (each step is the twelth root of 2 apart) has imbedded in its nomenclature and traditions all the complexities of the many centuries of its evolution. Unfortunately, consonance suffered for the simpicity of the Western scale, and only the intervals of the forth and fifth remain at minimum possible dissonances.
Bells have generally been excluded from Western instrumental ensembles because their inharmonic timbres produced dissonances with other instruments. Carillons (large bell instruments) have had similar problems which will be discussed in the next section. The invention of the harmonic bell has solved all of the problems associated with achieving the desired consonance using bells.
- THE EVOLUTION OF MODERN BELLS
Musical bells of an almond shaped plan (called nau) have been known in China since the SHANG Dynasty from the 15th century century BC and are found as musically tuned sets from the CHOU dynasty (1027 to 256 BC) during which both Taoism and Confucianism were founded and the use of bells a heightened part of courtly life.
Large, round (or axis-symmetric) bells are believed to have evolved in India and found a place in the traditions and rituals of Hinduism and later, Buddhism. This tradition made its way gradually through the nomadic steppes tribes into China from the fall of the HAN dynasty in 220 AD and the division of China into warring parts. Buddhism began to replace Confucianism as the state religion. While the bell, as an important religious object, languished in India under the long reign of Islam from the 2nd Century AD, in Buddhist China the single axis-symmetric bell grew in both scale and significance. The consolidation of China under the T'ANG dynasty from 620 AD consolidated the Buddhist bell in China. We have no significant Buddhist bells in China which predate the sixth century. This use of a single bell as a religious instrument relegated the Chung pein, a set of tuned bells used as a musical instrument, to a small part of the tradition of the temple. The technology of casting larger and larger bells swept through Korea and China, and then spread, in the same century, from Korea into Japan along with the Buddhist faith.
Very little information is available on aesthetic values pertaining to the sound of Asian temple bells and how these bells may have evolved in relatively recent times. Australian Bell has established a data base of Asian bell sounds and profiles, but much more detailed investigations including interviews with monks who use these bells, will need to be done before more systematic knowlege can emerge.
|
|
|
Ancient Chinese 2-tone musical bells
|
A Korean temple bell
|
A Korean temple bell spectrum
|
The European bell tradition is thought to have begun in the ancient Middle East with crotal bells and small clappered bells used on clothing and horse harnessing to protect the wearer from evil spirits. Large cast bronze bells have been known in churches since the early medieval times of Charlemaine in Europe. This art was largely confined in use to the rituals of the Christian religion. The art of casting bronze bells was a monastic practice until the late renaissance when in both Continental Europe and England a growing musical interest in the bell promoted the development of groups of bells into musical instruments.
This growing secular appreciation of the bell as a musical instrument took the form of change ringing the swinging bell in England, and the construction of a keyboard (clavier) to mechanically play bells in a carillon in the Low Countries. The invention of the carillon in the mid 1500's AD, especially encouraged an interest in controlling more exactly the tuning of the individual bell and the tuning relationship between a group of bells. In Flanders during the 1630's a court musician Van Eyck, worked with the Hemony Brothers bellfounders to produce the first well-tuned musical bells for use in carillons.
The Hemony Brothers were able to distinguish and tune the first three overtones of their bells. They were able to tune the second overtone to twice the frequency of the fundamental, but the third overtone could only be tuned to the musical interval of a minor third (2.4 times the frequency of the fundamental).
The secret of tuning bells became gradually lost after the death of the Hemony bellfounders. It was rediscovered around the early 1890's when a bell enthusiast, Cannon Simpson worked with the English bellfounders, Taylors at Loughborough. The secret was not to try and cast a bell in tune (called a maiden casting if successful) but to cast the bell thicker than was required and using a lathe to cut away metal from inside the bell until the overtones were sounding in their proper tuned sequence of the first five overtones of the bell at frequencies 2, 2.4, 3 and 4 times the fundamental.
|
|
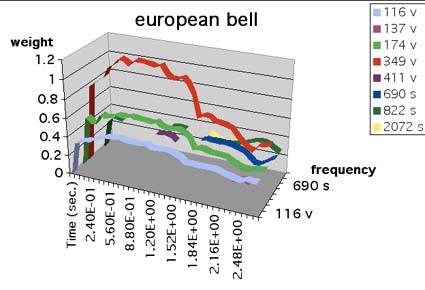 Calculated pitch percepts for the spectrum shown opposite. The strong fundamental percept at 349 Hz diminishes after 1.5 seconds and is overtaken by the minor third percept at 822 Hz. The 690 Hz partial only dissociates from the 349 Hz fundamental after 1.5 seconds which probably contributes to the rapid decrease in the 349 Hz pitch weight. The 137 Hz percept is the common subharmonic of both the 2nd and 3rd (minor 3rd) partials. It only appears at maxima of the minor third. Calculated pitch percepts for the spectrum shown opposite. The strong fundamental percept at 349 Hz diminishes after 1.5 seconds and is overtaken by the minor third percept at 822 Hz. The 690 Hz partial only dissociates from the 349 Hz fundamental after 1.5 seconds which probably contributes to the rapid decrease in the 349 Hz pitch weight. The 137 Hz percept is the common subharmonic of both the 2nd and 3rd (minor 3rd) partials. It only appears at maxima of the minor third.
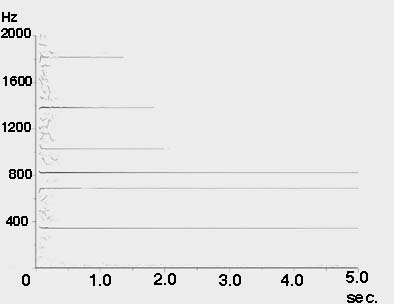
European minor 3rd bell spectrum |
This produced bells with a strong pitch perception based on the fundamental. However the minor third overtone has a large amplitude and Terhardt, in his paper on pitch perception, reported that in about 30% of trials people reported the pitch of a European bell to be the minor third overtone.
The minor third overtone was also a problem for carillons because it produced strong dissonances with the overtones of a bell playing at an interval of a major third. This is the second most common interval in Western music, so in the 1980's a Dutch foundry, Eisbouts, collaborated with Dr Schoofs from Eindhoven Technical University to design a bell with a major third overtone instead of the minor third. This was achieved by using a new computer modeling technique called Finite Element Analysis (FEA) to predict the frequencies of the overtones of computer models of bell with varying shapes.
In 1999 Australian Bell was commissioned by the Melbourne International Festival of the Arts to design and manufacture a set of large bells to comemorate the centenary of Australia's Federation. These bells were designed using very recent FEA with shape optimisation software (ReShape) produced by Advea Engineering. The world's first harmonic bell with seven partials in an harmonic series, along with a series of bells producing two and even three clearly perceived pitches, were designed and cast for this commission.
|

.jpg)

.jpg)